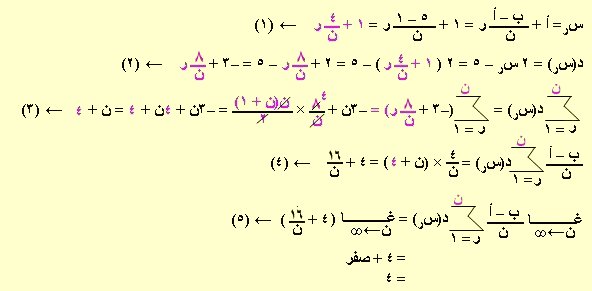
الفترة [ 1 ، 5 ] = [ أ ، ب ]    ، د(س) = 2 س – 5

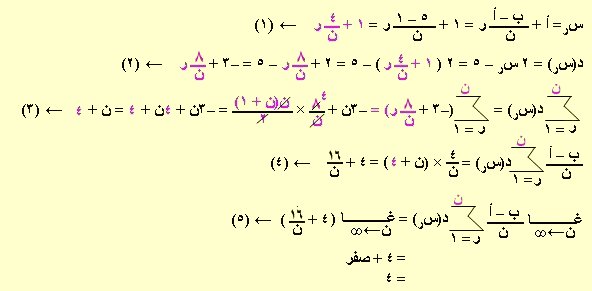
باستخدام المساحة

نوجد قيم د(5) ، د(1)

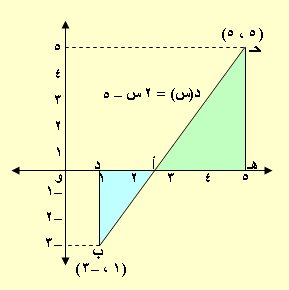
د(5) = 2 × 5 – 5 = 10 – 5 = 5  والنقطة ( 5 ، 5 )

د(1) = 2 × 1 – 5 = 2 – 5 = –3 والنقطة ( 1 ، –3 )

نرسم منحنى الدالة الذي يمثله ب حـ ( خط مستقيم) يقطع محور السينات عند س = 2.5

من : بوضع د(س) = 0 فإنَّ 2 س –  5 = 0 أي س = 2.5

من المعلوم المساحة فوق محور السينات موجبة وأسفله سالبة

والمساحة تحت منحنى د(س) =2س –5 ومحور السينات والمستقيمان س= 1 ، س= 5

هي مجموع مساحتي المثلثين ب د أ ، أ هـ حـ جبرياً

مساحة المثلث ب د أ = 0.5 × 1.5 × 3 = 2.25 وحدة مساحة

مساحة المثلث أ هـ حـ = 0.5 × 2.5 × 5 = 6.25 وحدة مساحة

المساحة المطلوبة = 6.25 – 2.25 = 4 وحدة مساحة

  5

 ∫ ( 2 س – 5) د س = 4     وهي نفس النتيجة باستخدام التجزيء النوني المنتظم

  1