التكامل المحدود كنهاية مجموع
بالعودة لتجزئة الفترة السابق ذكرها المبينة هنا مع الشكلين حيث نتوصل لتعريف التكامل المحدد كنهاية مجموع.
ــــــــ.ــــــــــ.ــــــــــــــــــــــــــــــــــ.ـــــــــــــ.ــــــــــــــــــــــ.ـــــــــــ.ــــــــــــ.ـــــــــــ.ـــــــــــ.ــــــــــ جزء من خط الأعداد الحقيقية (ح) أو محور السينات
ب=سن سن–1 سر سر–1 س4 س3 س2 س1 س0= أ
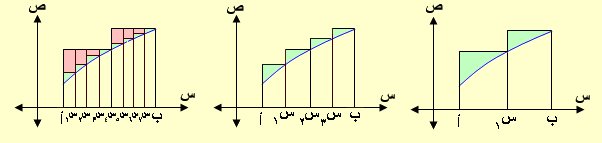
هذه التجزيئات للفترة [ أ ، ب ] والتي سنقدم الشكل الآتي الذي يبين تجزئ الفترة عند نقطة س1 للحصول على مستطيلين الشكل الأول والنقاط
س1 ، س2 ، س3 للحصول على 4 مستطيلات (الشكل الثاني) والنقاط من س1 إلى س7 للحصول على 8 مستطيلات

ففي الشكل الأول المساحة تحت المنحنى أقل من مجموع مساحتي المستطيلين بفارق الجزء المظلل باللون الأخضر
وفي الشكل الثاني زدنا تجزئ الفترة والمساحة تحت المنحنى أقل من مجموع مساحات المستطيلات الأربع بفارق الجزء المظلل باللون الأخضر
وفي الشكل الثالث زدنا تجزئ الفترة والمساحة تحت المنحنى أقل من مجموع مساحات المستطيلات الثمانية بفارق الجزء المظلل باللون الأخضر
لاحظ أن مساحة الجزء الأخضر في الشكل الأول > مساحته في الشكل الثاني > مساحته في الشكل الثالث
لاحظ أيضاً رؤوس أشباه المثلثات المظللة تقترب من المنحنى أكثر في الشكل الثالث عنها في الشكل الثاني أي بزيادة التجزيء تنقص المساحة
المظللة وتقترب رؤوس أشباه المثلثات المظللة من المنحنى ومن الواضح إذا زادت التجزئة إلى مالانهاية من التجزيئات فإن المساحة المظللة تصبح صفراً وتلك النقاط تنطبق على المنحنى أو بمعنى أكثر دقة تكون المساحة تحت المنحى مساوية لمجموع مساحات المستطيلات والآن لننظر للشكل التالي حيث سنصل منه لتعريف التكامل المحدد كنهاية مجموع

ب – أ
بتقسيم الفترة [أ ، ب] ن فترة متساوية (تجزيء نوني منتظم) طول كل منها ـــــــــــــــ وهذا الطول يمثل القاعدة لأي مستطيل والمبين بالشكل
ن
باللون الأزرق الفاتح أو اللون الأخضر الفاتح أما عن ارتفاع هذه المستطيلات(البعد الثاني لأي مستطيل) فهو يمثل قيمة الدالة عند نقطة التجزيء أي
ب – أ
د(س1) ، د(س2) ، ... د(سر) حيث سر = أ + ــــــــــــ ر ، لنحسب المساحة الآن (المنطقة المضلعة بدءاً من أ مرور برؤوس المستطيلات العلوية
ن
حتى ب على محور السينات بالنسبة للشكل جهة اليمين).
مساحة المنطقة المضلعة = (س1 – س0) × د(س1) + (س2 – س1) × د(س2) + ... + (سر– سر–1)× د(سر) + ... +(سن– سن–1)× د(سن)
ب – أ ب – أ ب – أ ب – أ
= ــــــــــــــــ × د(س1) + ــــــــــــــــ × د(س2) + ... + ــــــــــــــــ × د(سر) + ... + ــــــــــــــــ × د(سن)
ن ن ن ن

يعرف هذا بالمجموع العلوي النوني ويرمز له بالرمز عن ولو قمنا بالمثل بالنسبة للشكل الأيسر أعلاه سنحصل على المجموع السفلي النوني ويرمز له بالرمز سن ، فإذا حسبنا الغاية لكل منهما عندما ن تقترب من ∞ ففي حالة تساويهم نقول الدالة قابلة للتكامل ويكون التكامل المحدد كمجموع نوني :


يراجع قوانين السيجما
تنبيـه :
إذا قلنا ∆ س هو طول الفترة الجزئية مقدار التغير في س كطول فيكون د(س) × ∆ س مساحة مستطيل بعداه د(س) ، ∆ س وعلى ذلك يكون :
ب
∫ د(س) د س يعبر عن المساحة المحدودة بمنحنى ص = د(س) ومحور السينات ، والاحداثيين الرأسيين س = أ ، س = ب
أ
وإن كانت د(س) تدل على السرعة ، ∆ س تدل على الزمن فحاصل ضربهم يدل على المسافة المقطوعة في زمن قدره ∆ ن وعلى ذلك يكون :
ب
∫ د(س) د س يعبر عن المسافة المقطوعة أثناء الفترة الزمنية ( ب – أ )
أ
وإن كانت د(س) تدل على قوة ، ∆ س تدل على إزاحة في اتجاه القوة فحاصل ضربهم يدل على الشغل المبذول في المسافة ∆ س وعليه يكون :
ب
∫ د(س) د س يعبر عن الشغل المبذول في المسافة ( ب – أ ) وهكذا .....
أ
يعرف هذا القانون أو تعريف التكامل المحدد بقانون التجزيء النوني المنتظم فتحققه يعني الدالة قابلة للتكامل على الفترة [ أ ، ب ] أي هو طريقة لإثبات أن الدالة قابلة للتكامل على فترة أم لا أما كون الدالة قابلة للتكامل فهو محقق ولذا يستخدم في الغالب للدوال القابلة للتكامل والدالة المتصلة في فترة مغلقة تكون قابلة للتكامل على هذه الفترة