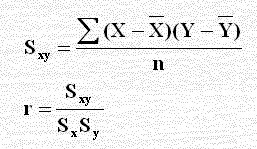
طريقة معامل التغاير
نكون الجدول الآتي لاستخدام معامل التغاير (Covariance) لحساب قوة العلاقة وهي طريقة قل استخدامها ويحسب معامل التغاير Sxy من القانون الآتي ومنه نحسب معامل الارتباط r كما مبين بالآتي:
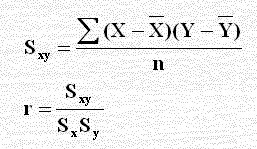
|
X |
Y |
X – `X |
Y – `Y |
(X – `X)(Y – `Y) |
| 6 | 4 | – 3.44 | – 3.89 | 13.382 |
| 8 | 8 | – 1.44 | 0.11 | – 0.158 |
| 7 | 6 | – 2.44 | – 1.89 | 4.612 |
| 14 | 10 | 4.56 | 2.11 | 9.622 |
| 11 | 9 | 1.56 | 1.11 | 1.732 |
| 12 | 11 | 2.56 | 3.11 | 7.962 |
| 8 | 8 | – 1.44 | 0.11 | – 0.158 |
| 9 | 7 | – 0.44 | – 0.89 | 0.392 |
| 10 | 8 | 0.56 | 0.11 | 0.062 |
| 9.44 | 7.89 | 0.04 | 0 | 37.444 |
نحسب كل من Sx , Sy كما سبق في حل آخر وكالتالي:
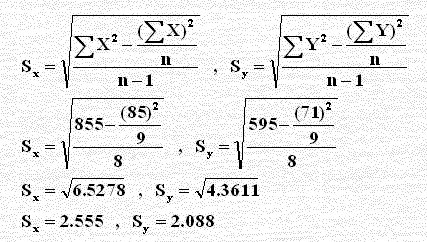
بتطبيق القانون نجد أنَّ:
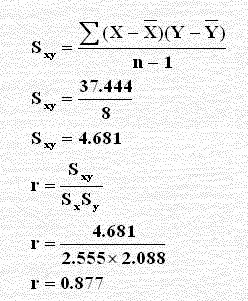
وهو نفس قيمة معامل الارتباط في الحل السابق ونفس الاختبار السابق ذكره.