Use MathCad to Solve:  e-x - e2x + 1 = 0  ¾®			e-x - e2x + 1 = 0 solve ® 0.28119957			لاحظ في حل المعادلة (MathCad 18) حصلنا على الجواب الحقيقي ¾¬
	By: Mathematica 9		By: Derive 6		By: MathCad 15			By: Maple 18		By: Excel
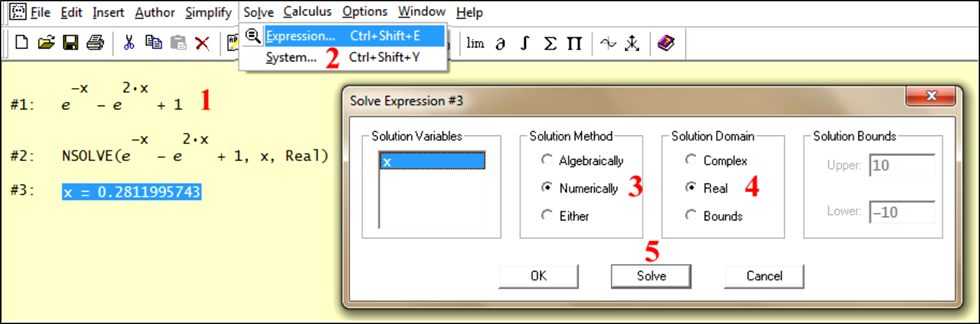
	NSolve[E^(-x) -E^(2x)+1, {x},Reals,8]		NSOLVE(e-x- e2x+1, x, Real)		Ctrl+Shift+. Before solve, Ctrl + = To have =			fx := exp(-x)-exp(2x)+1 = 0:		See Example 10
	{{x ® 0.28119957}}		0.28119957		e-x - e2x + 1 = 0 solve ® 0.28119957			fsolve(fx)		By Secant &
			↓↓↓	↓↓↓				0.28119957	Decimal = 8	By Newton
	MthLab 11, 15 (Also)
	numeric::solve(exp(-x)-exp(2*x)+1=0)
	{[x = 0.2811995743]}