الصورة العامة لمعادلة الدرجة الثانية في متغيرين س ، ص هي

أ س² + ب س ص + حـ ص² + د س + هـ ص + ك = 0 ← (1)

في حالة أ = حـ ، ب = 0 فتؤول المعادلة (1) لمعادلة دائرة

في حالة ب = 0 فتؤول المعادلة (1) للصورة أ س² + حـ ص² + د س + هـ ص + ك = 0 ← (2)

المعادلة (2) تمثل معادلة قطع ناقص إذا أ حـ > 0 وتمثل معادلة قطع زائد كون أ حـ < 0

في حالة كون ( حـ = 0 ، د = 0 ) أو ( أ = 0 ، هـ = 0 ) فتمثل المعادلة (2) قطع مكافئ

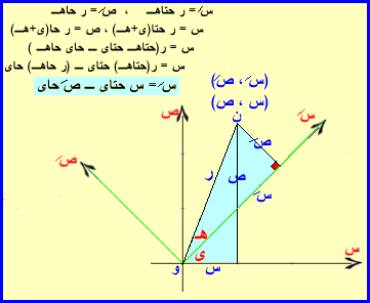
يمكن حذف الحد المشتمل على س ص في المعادلة (1) بدوران المحاور بزاوية ى أي د(و،ى) فنحصل على معادلة جديدة ضمن المحاور الجديدة س^/ ، ص^/ ومن الشكل الآتي نجد أن:

علماً بأن معادلتي الدوران هما

س = س^/ حتاى – ص^/ حاى ، ص = س^/ حاى + ص^/ حتاى ← (2^/)

وبالتعويض نحصل على أ^/ س^/2 + ب^/ س^/ ص^/ + حـ^/ ص^/2 + د^/ س^/ +هـ^/ ص^/ + ك^/ = 0 حيث أن أ^/ = أ حتا^2ى + ب حاى جتاى + حـ حا^2ى ب^/ = ب( حتا^2ى – حا^2ى ) + 2( حـ - أ) حاى جتاى ← (3) حـ^/ = أ حا^2ى – ب حاى جتاى + حـ جتا^2ى د^/ = د حتاى + هـ حاى ، هـ^/ = هـ حتاى – د حاى ، ك^/ = ك وينعدم الحد س ص في حال ب^/ = 0 ومن (3) نحصل على طا2ى = ب / ( أ – حـ ) ، أ ≠ حـ ، ى = 45^ه حال أ = حـ ، ب ≠ 0 ← (4) ولحل هذا النوع من المسائل(المشتمل على س ص ) يجب تعيين قيمة ى من (4) ، س ، ص من (2^/) والتعويض في المعادلة. مثال ذلك :  س ص = 2 أ = حـ = 0 ، ب = 1 فإن ى = 45^ه ،وبالتعويض في معادلتي الدوران س = س^/ حتاى – ص^/ حاى¬ س = ½ (2 ^½) س^/ - ½ (2 ^½) ص^/ س = س^/ حتا45 – ص^/ حا45

ص = س^/ حاى + ص^/ حتاى ¬ ص = س^/ حا45 + ص^/ حتا45 ¬ ص = ½ (2 ^½) س^/ + ½ (2 ^½) ص^/

بالتعويض في س ص = 2 عن س ، ص نحصل على:[ ½ (2 ^½) س^/ - ½(2 ^½) ص^/ ][ ½ (2 ^½) س^/ - ½(2 ^½) ص^/ ] = 2

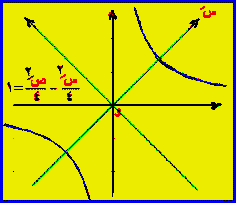
س^/2 / 4 – ص^/2 / 4 = 1 ، وهي معادلة قطع زائد بؤرتاه على المحور و س^/