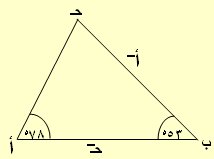
مثال: أ ب حـ مثلث فيه < ب = 53^ه ، < أ = 78^ه فإذا كانت مساحة المثلث أ ب حـ تساوي 53.62 سم² فأوجد طول ب حـ

الحل: نعلم أن مساحة المثلث = نصف حاصل ضرب ضلعين في جيب الزاوية بينهم فمن الشكل نجد أن:

                                         1

        مساحة المثلث أ ب حـ = ــــ  أ^‾ حـ^‾ حـا ب  ........... (1)

                                        2

                              أ^‾        حـ‾  

    من قاعدة الجيب: ــــــــ = ــــــــــــ        .................................. (2)

                           حا أ      حا حـ

   < حـ = 180 − ( 53 + 78) = 180 − 131 = 49^ه   "مجموع زوايا المثلث = 180"

          التعويض في (1) ، (2)

                       1

        53.62 = ــــ  أ^‾ حـ‾ حـا53^ه  ........... (3)            من (1)

                       2

             أ^‾           حـ‾

        ــــــــــــــ = ــــــــــــــ        .................................. (4)    من (2)

        حا 78       حا 49

                        أ^‾حا 49

       منها: حـ‾= ـــــــــــــــــــــ        .................................. (5) 

                        حا 78

       بالتعويض من (5) في (3) نحصل على:

                       1            أ^‾حا49

        53.62 = ــــ × أ^‾× ـــــــــــــــــ × حـا53^ه     وباستخدام الآلة الحاسبة يكون:

                       2            حا78

                       1           أ^‾ × ـ0.7547

        53.62 = ــــ × أ^‾× ــــــــــــــــــــــــــــ × 0.7986     ومنها نحصل على:

                      2              0.9782

                    2 × 53.62 × 0.9782

          ( أ^‾)^ـ2= ـــــــــــــــــــــــــــــــــــــــــــــــ = 174.05 تقريباً    ومنها   أ^‾ـ= 13.19 سم تقريباً  ، أي: ب حـ =13.19سم

                     0.7547 × 0.7986  

تنبيه1: من المعادلة (4) يمكن حساب  حـ‾ حيث  حـ‾ـ = 13.19 × حا49 ÷ حا78 = 10.18سم

تنبيه2: للتأكد من (1) مساحة المثلث = 0.5 × 13.19 × 10.18 × حا53 = 53.62سم² "المساحة المعطاة"