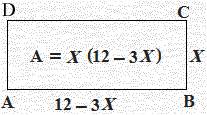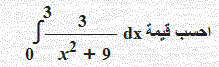أجب عن جميع أسئلة هذا الامتحان وعددها ( i( 8                                                            الدرجة النهائية i100

الملاحظات

الامتحان

 i10 درجات  , درجتان لكل فقرة

i1) نجزىء الكسر لكسرين مع ملاحظة أنَّ 

         tan x

  lim ——— = 1

 x→0    x

         X + tan X                X                 tanX 

  lim  ————— = lim —— +   lim ———

X→0        X             X→0  X        X→0    X 

                        = 1 + 1 = 2

i2)انعلم أنَّ: مشتقة (i(sinX/2هي (i½ )cos(X/2)

ƒ^\(X) = (i1/2)cos(X/2)  ƒ^\(p) = (i½)cos(p/2)

          = (½)×0 = 0

 i3) ميل المماس عمودي على مستقيم ميله i−1فميل المماس

      هو i1لأن حاصل ضرب ميلي مستقيمين متعامدين هوi−1

       ميل المماس هو المشتقة الأولى أي (ƒ ^\ (x₁ ويكون:

ƒ ^\ (x₁) = 1

i4) نطبق خاصية الجمع لتكامل دالتين ( التوزيع )

∫(ƒ(x)+2x ) dx=∫ƒ(x) dx +∫2x dx

     تكامل i2xفي الفترة والناتج i21

     تنقل i21للطرف الأيسر والناتج للتكامل يكون i−4

     تبديل حدي التكامل يغير إشارة قيمة التكامل .

      ناتج التكامل = i4

i5) المتباينة  ib > 2تعني i|x| = xفتصبح الدالة i3x²

     بالتكامل والتعويض يكون ib³ − 8= 56

      نحل المعادلة

b = 4

—————————————

i13 درجة  , i1) خمسة , i2) أربعة , i3) أربعة

i1) الزاوية x = 45^o فيكون

 y = csc²(45^o) = 2 , z = 2³ = 8

     نشتق z , y (مشتقة الدالة الأسية تساوي الأس مضروب

     في الدالة بأس −1 في مشتقة الأساس

f(x) = (g(x))ⁿ   f^\(x) = n(g(x))^n-1 g^\(x)

     نطبق قاعدة التسلسل

     التعويض والجواب مع ملاحظة:

−6 y² csc²x cotx =−6 y³ cotx =−6×8=−48

i2)  نشتق

      نضع x = 2 لأنها تحقق x³ + 1 = 9

      أو حل المعادلة x³ + 1 = 9 للحصول على قيمة x

      بالتعويض عن x= 2

i3) نوجد المشتقة الأولى

     الاستقاق لدالة ضمنية وكذلك لحاصل ضرب دالتين

     (5xy)^\ = 5xy^\ + 5y

         بالتعويض

      المعادلة : (y − y₁ = m (x − x₁

      الاختصار

      المطلوب

—————————————

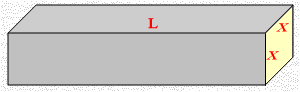
i9 درجة  , i1) خمسة درجات , i2) أربعة درجات

i1) المقطع شكل مربع , القضيب على شكل متوازي مستطيلات

      حجم متوازي المستطيلات V حيث: V = x² L

      كل من V, x, L مرتبط بالزمن والاشتقاق هنا للطرف

      الأيسر كحاصل ضرب دالتين والاشتقاق هنا بالنسبة للزمن

      الأول × مشتقة الثاني + الثاني × مشتقة الأول

  1 m = 100 cm , V^\ هو معدل التغير في الحجم  

L^\ معدل التغير في طول القضيب , x^\ معدل التغير في ضلع القاعدة

i2) مشتقة المسافة S تعطى السرعة V، مشتقة السرعة تُعطي

     العجلة A . أو المشتقة الثانية للمسافة ^\\ S يُعطي العجلة.

     مشتقة الدالة sin t هي cos t, مشتقة cos t هي sin t−

     cos p = cos(180^o) = −1

     sin 2x = 2sin x cos x  دالة ضعف الزاوية

—————————————

i15 درجة  , i1) تسعة درجات , i2) ستة درجات

i1) أكبر ما يمكن للمساحة يعني مشتقتها الأولي تساوي الصفر

     الشكل التالي يبين شكل المستطيل وأبعاده .

      مساحة المستطيل (A) تساوي الطول (BC)×العرض(AB)

     للتأكد من كون المساحة أكبر ما يمكن نتأكد من أنَّ المشتقة

     الثانية سالبة .

i2) ميل المنحنى هو المشتقة الأولى

     نقطة حرجة تعنى المشتقة عندها تساوي الصفر

     النقطة واقعة على المنحنى تعني تحقق معادلته

     بتكامل الميل أي المشتقة الأولى نحصل على y أي (ƒ(x

     نوجد ثابت التكامل من التعويض عن النقطة الحرجة

     نكتب معادلة المنحنى

—————————————

 i18 درجة

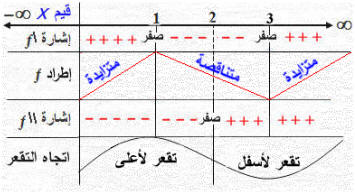
i1) نوجد المشتقة الأولى لتحديد فيترات التزايد والتناقص

     نحصل على قيم X التي عندها نقاط حرجة من ƒ^\(X)=0

     ونعوض عنها للحصول على قيم Y والنقاط الحرجة.

     نبحث إشارة ^\ƒ لمعرفة فترات التزيد والتناقص

     لاحظ: المقصود بإشارة X ² هنا معامل X ² وهي إشارة a

            في المعادلة aX ² + bX  + c = 0

            في صورة الخط المستقية aX + by + c = 0

            إشارة X تعني إشارة a

     الرسم أدناه يكتفى منه رسم المنحنى وإظهار النقاط فقط

     وغيره للتوضيح ولكن لا مانع منه

بالإمكان عمل الجدول الآتي ونستفيد منه في الحل.

للتفاصيل وبالعربية أضغط على الرابط الآتي:

http://jmasi.net/Math/analysisa/derivefm.htm

—————————————

i12 درجة  , ia) أربعة , ib) أربعة , ic) أربعة

ia) النسبة × مقلوبها = i 1

secx cosx = (1/cosx)cosx = 1

ia) تكامل الدالة الأسية × مشتقة أساسها هو الدالة الأسية بزيادة

     أسها i1صحيح وقسمتها على الأس الجديد(دالة × مشتقتها)

 ∫[f(x)]ⁿ f ^\(x)=[f(x)]ⁿ⁺¹/(n+1)

     ضربنا × ستة وقسمنا عليها للحصول على مشتقة الأساس

ic) لاحظ أنَّ : sin²x + cos²x =1

     نأخذ cos x عامل مشترك ونستبدل i1 − cos²xبما

     تساويه وهو sin²x - نطبق تكامل دالة × مشتقتها

 —————————————

 i13 درجة  , i1) أربعة , i2) تسعة    

i1) نطبق القاعدة

∫[f(x)]ⁿ f ^\(x)=[f(x)]ⁿ⁺¹/(n+1)

i2) بالمساواة نجد أنَّ: i2x − x² = −3ومنها نوجد قيم x

     وهي حدي التكامل للفرق بين المستقيم ومنحنى كما مبين

     بالشكل الآتي ( لا داعي لوجوده في الحل وإن كان الأفضل).

—————————————

   i10 درجة

i1) الحل بالتكامل بالتعويض بمعنى تحويل الدالة في المسألة

     لدالة قياسية يسهل تكاملها لذا نحول الدالة الجبرية في X

     لدالة مثلثية وذلك بوضع

X = 3 tanq

   → التعويض هنا لحدي التكامل والدالة و dx  

—————————————

السؤال الأول:

اختر رمز الإجابة الصحيحة في كل مما يأتي , علماً بأنه توجد إجابة صحيحة واحدة من بين البدائل الأربع التي تلي كل فقرة :

    X + tan X            

    ؟  lim  —————   ما القيمة (i1

    X→0        X                      

                                                              1

 2   (D                       1    (C                   —    (B                        0    (A 

                                                              2

                                          ü

                     X  

i2) إذا كانت ƒ(X) = sin —i , فما قيمة ( ƒ^\( p 

                 i2

                                                                     1                                                               1

−1   (D                      − —  (C                  0   (B ü                    —    (A      

                   i2                                                               2

i3) إذا كان المماس لمنحنى ( y = ƒ(X عند النقطة (x₁ , y₁) الواقعة على المنحنى , وعمودياً على المستقيم

     x + y = 4 , فمل قيمة (ƒ ^\ (x_{1 .}

      i   (D                          1    (C  ü           0   (B                       −1     (Aغير معرفة

                                      2                        5

i4) إذا كان i( ƒ(x) + 2x) dx = 17∫, فما قيمة ƒ(x) dx∫   ؟

                          5                        2

ا

                              −4   (D                      4    (C ü                    11   (B                     25  (A

الحل

      5                                  5                   5               5                                     5

i4)  ∫(ƒ(x)+2x ) dx=17 →∫ƒ(x) dx + x²│= 17 →∫ƒ(x) dx+(25−4) =17→∫ƒ(x) dx =−4

     2                                  2                    2             2                                      2                   

       2                           

      ∫ƒ(x) dx = −(−4) = 4

     5

                                                  b

i5) إذا كان ib > 2, وكان i3 x |x| dx = 56∫  فما قيمة b ؟

                                   2

 7   (D                      6    (C                         5   (B                      4  (A ü   

       b                             b       

      ∫3x² dx = 56 → x³│= 56 →b³ − 8 = 56 → b³ = 64 → b = 4

     2                               2

—————————————

السؤال الثاني:

                             p           dz

i1) إذا كان y = csc² x ،اz = y³ فأوجد — عندما  — = x

                              4            dx

  الحل

   dz        dz        dy

 —— = —— . —— 

   dx        dy      dx

   dz

 —— =3y² . 2cscx(−cscx cotx) = −6 y² csc²x cotx

   dx

   dz

 —— =−6 y² csc²x cotx   [ y = csc²(45^o) = 2 , cot(45^o) = 1 ,  ]

   dx

   dz

 —— =−6×4×2×1 = −48

   dx

       │     p

         x=—

               4

i2) إذا كانت (ƒ(x قابل للاشتقاق . وكانت ƒ(x³ + 1) = 12x فأوجد (iƒ^\(9.

 الحل

     بالاشتقاق i 3x² ƒ^\(x³ +1) = 12, وبوضع x = 2 نجد أنَّ:

3×4ƒ^\(8 +1) = 12 → 12ƒ^\(9) = 12  → ƒ^\(9) = 1

                                       dy

i3) إذا كانت ix² − 5xy − y² = 7فأوجد —— عند ( i1 , −2) الواقعة على منحناها .

                                       dx

  الحل

             dy                dy

2x − 5x — − 5y −2y — = 0          (i1 , −2 ) بالتعويض عن النقطة

             dx                dx

                 dy                           dy

2×1 − 5×1 — − 5×−2 −2×−2 — = 0

                 dx                           dx

            dy                  dy                  dy

2 − 5 —— + 10 +4 —— = 0 → ——  = 12

            dx                  dx                  dx

  dy  

——  = 12

  dx│_(1,−2)

—————————————

السؤال الثالث:      

i1) سُخن قضيب معدني مصمت (غير مجوّف) مقطعه على شكل مربع , فازداد طول القضيب بمعدل

    i0.01 cm/min, وفي الوقت نفسه ازداد طول ضلع مقطعه بمعدل  i0.005 cm/min, أوجد معدل

    التغيُر في حجم القضيب , عندما يكون طوله  i1 m, وطول ضلع مقطعه  i1.4 m 

الحل

بفرض أنَّ طول ضلع المقطع ixوطول القضيب L

V = x² L

V^\= x² L^\ +2x x^\ L

    = (1.4)²×0.01 + 2×1.4×0.005×100

    = 0.0196 + 1.4

    = 1.4596

  dV

 — =1.4596 cm³/min

  dt

i2) يتحرك جسيم على خط مستقيم مبتدأًّ من نقطة ثابتة وفقاً للعلاقة S = 8 sin² t حيث S هي المسافة المقطوعة بالامتار (m) ,

                    p

     t الزمن بالثواني (sec) . أوجد تسارع (عجلة) الجسيم بعد sec ـــــ من بدء الحركة .

                    2

                                                                             الحل

S = 8 sin² t → V = 8×2sin t cos t = 8 sin 2t

A= 16 cos 2t

A= 16 cos p =16 × −1 = −16 m / sec²

 │    p

   x=—

        2

—————————————

السؤال الرابع: 

i1)اABCD مستطيل فيه AB + 3BC = 12 cm , أوجد كلاً من AB , BC بحيث تكون مساحة المستطيل أكبر ما يمكن .

     الحل

     بفرض أنَّ  BC = X فإنّ َ AB = 12 − 3X

A = X (12 − 3X) = 12X − 3X ²

A^\ = 12 − 6X

 o = 12 − 6X

 X = 2

 BC = 2 cm , AB = 12 − 3×2 = 12 − 6 = 6 cm

A^\\ = − 6 → المساحة أكبر ما يمكن

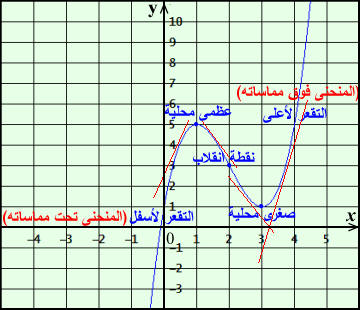
i2) إذا كان ميل المماس لمنحنى (y = ƒ(X  عند أي نقطة (X  , y) واقعة عليه هو m = aX − 8 حيث aÎR ,

     فأوجد كلاً من قيمة a ومعادلة المنحنى , علماً بأنَّ (i(4 , 1نقطة حرجة على المنحنى .

الحل

m = aX − 8 → 0 = a×4 − 8 بالتعويض عن النقطة الحرجة

0 = 4a − 8 → a = 2

m = 2X − 8 = y^\

y =∫ (2X − 8) dX  = X² − 8X  + C  (C ثابت التكامل)

y = X² − 8X  + C     بالتعويض عن النقطة المعطاة لأنها واقعة على المنحنى

1 = 16 − 32 + C → C = 17

y = X² − 8X  + 17

     —————————————

السؤال الخامس:

     إذا كانت ƒ(X) = X³ − 6X ² + 9X + 1 ,

i1) أوجد فترات التزايد وفترات التناقص للدالة ƒ ( إن وجدت ).

i2) أوجد القيم العظمى والقيم الصغرى المحلية للدالة ƒ ( إن وجدت ).

i3) أوجد فترات التقعر إلى أعلى وفترات التقعر إلى أسفل ونقاط الانقلاب للدالة ƒ ( إن وجدت ).

i4) مثل الدالة بيانياً بصورة تقريبية في المستوى الإحداثي أدناه.

الحل

ƒ^\ (X) = 3X ² −12X + 9 → 0 = 3(X ² −4X + 3) → 0 = (X −1)(X − 3)

X = 1 , X = 3       عندها نقاط حرجة

ƒ(1)=1−6+9+1=5 , ƒ(3)=27−54+27+1=1 , (1 ,  5) , (3 , 1)  نقاط حرجة

         الدالة ƒ متناقصة في [ i[ 1 , 3, ومتزايدة  في ( ¥i(−¥ , 1 ] , [ 3 ,i

     للدالة ƒ قيمة صغرى محلية عند (i(3 , 1(تغيرت إشارة الدالة قبل i3عن بعد i3من سالب لموجب).

     للدالة ƒ قيمة عظنى محلية عند (i(1 , 5(تغيرت إشارة الدالة قبل i1عن بعد i1من موجب لسالب).

ƒ^\\ (X) = 6X − 12 → 0 = 6(X − 2) →X = 2 → ƒ(2) =8−24+18+1 = 3 →  (2 , 3)  نقطة انقلاب

المنحى ƒ مقعر لأسفل في ( i(−¥ , 2, ومقعر لأعلى في ( ¥i ( 2 ,i

ƒ(0) = 1 , ƒ(4) = 64 − 96 + 36 + 1 = 5  لإيجاد نقاط إضافية

  (0 , 1) , (4 , 5)  نقاط إضافية لرسم المنحنى

—————————————

السؤال السادس:

     أوجد كلاً مما يأتي:

 a) ∫sec x cos x dx = ∫dx = x + c       النسبة × مقلوبهاi = 1

b) ∫(x² + 1)(2x³ + 6x + 1)⁶ dx = ¹/₆ ∫(6x² + 6)(2x³ + 6x + 1)⁶ dx

1       (2x³ + 6x + 1)⁷

= — × ———————— + c

6                   7

1

= — (2x³ + 6x + 1)⁷ + c

42

  c) ∫( cos x − cos³x )dx = ∫cos x(1 − cos²x )dx =∫cos x(sin²x )dx

            sin³x                 

       = ——— + c

                   3  

—————————————

السؤال السابع:

                                            ip

                                           —

                                            i4

i1  ) احسب قيمة  tan³  sec² x dx∫

                                       i0  

(tan x)^\ = sec² x

   p                                             p

  —                                            —

  i4                                              4

 ∫tan³ x sec² x dx = ¼ [ tan⁴ x ] = ¼ ( 1 - 0) = ¼

0                                                 0  

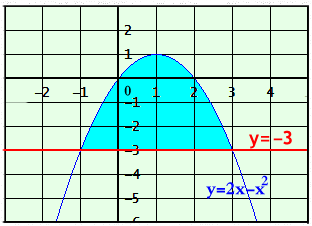
i2) أوجد مساحة سطح المنطقة المحصورة بين منحنى y = 2x − x² , والمستقيم y = −3 .

     الحل

2x − x² = −3 → x² − 2x − 3 = 0 → (x − 3)(x + 1) = 0 → x =−1 , x = 3    حدي التكامل

y₁ − y₂ = ( −3 ) − ( 2x − x² ) = −3 − 2x + x²

           3                                                                      3

A =│∫( 2x − x² −(−3 )) dx│=│[ x² − x³/3 + 3x]│

        −1                                                                     −1

                                       =│[ 3² − 3³/3 + 3×3] −[ (−1 )² − (−1 )³/3 + 3(−1)]│

                                       =│9 −9 + 9 −1 − 1/3 + 3│

                                                        32

                                        = —— وحدة مربعة

                                              3

—————————————

السؤال الثامن:

الحل

x = 3 tanq    بوضع

x = 0 → 0 = 3 tanq → tanq  = 0 → q = 0

x = 3 → 3 = 3 tanq → tanq  = 1 → q = p/4

x = 3 tanq  → dx = 3 sec²q dq

x² + 9 = 9 tan²q  + 9 = 9(tan²q  + 1) = 9 sec²q

    i3                       p/4                                       p/4

             3                          3                

  ∫ ———— dx = ∫ ————× 3 sec²q dq  = ∫dq

0       x² + 9           0      9 sec²q                          0    

                                p/4

                       = │q │

                                   0

                       =  p/4 − 0

                       =  p/4

—————————————